Research Findings

Most of our findings are now published. We summarize the highlights here.

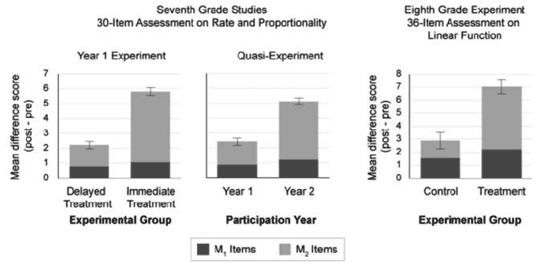
Across three large-scale studies, we replicated a strong main effect demonstrating that SimCalc enables a wide variety of teachers in a diversity of settings to extend students’ learning to more advanced mathematics. For the seventh-grade study, the seventh-grade quasi-experiment (delayed treatment teachers across years 1 and 2), and the eighth-grade study, the main effects were statistically significant and showed that students in the treatment group (or year 2) learned more than students in the control group (or year 1). HLM revealed main effects with student-level effect sizes of .63, .50, and .56, respectively.

Across all three studies, the gains difference between the two groups occurred mostly on the portion of the tests that indicate the SimCalc interventions create an opportunity to learn advanced mathematics beyond the typical curriculum. The student-level effect sizes of the portion of the test consisting of items that tested mathematics beyond what is covered at grade level (M₂) were .89, .69, and .81, respectively. In contrast, the student-level effect sizes of the portion of the tests consisting of items that tested mathematics typically covered at grade level (M₁) were .10, .13, and .19, respectively. This effect was significant only at the 0.05 level in the seventh-grade quasi-experiment and not at all in the other studies.
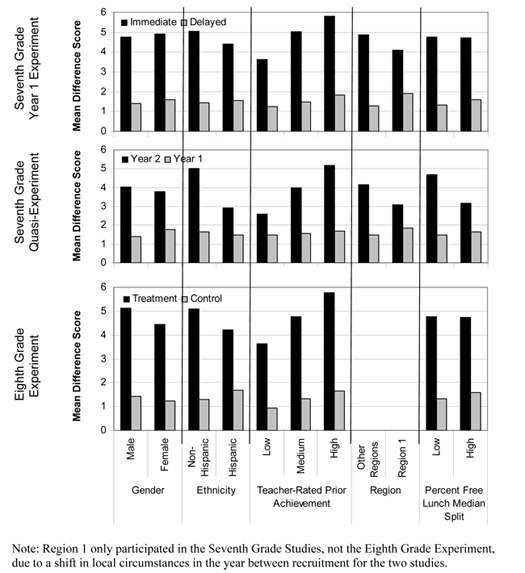
In both the seventh- and eighth-grade experiments, these student learning effects, particularly on the advanced portions of the tests, were robust across demographic groups, despite marked group differences at pretest. In the seventh- and eighth-grade experiments, we ran a series of hierarchical linear models predicting M₂ pretest and M₂ gains. Inserted as covariates in each model were experimental group, demographic factor, and the factor by group interaction.

Findings:

Gender. Whereas boys started out with higher pretest scores, boys and girls had similar gain scores.
Ethnicity. Considering the two major ethnic groups represented in our study, although Caucasian students started out with higher pretest scores, Hispanic and Caucasian students had similar gain scores in the two main experiments. In the seventh grade quasi-experiment, however, there was an interaction such that Hispanic students using SimCalc in Year 2 had lower learning gains than their non-Hispanic counterparts.
Teacher-rated prior achievement (low, medium, and high). In all three studies, students at all three levels gained more in the SimCalc replacement unit than their peers studying the ordinary curriculum; however, there were also interactions in the seventh-grade studies (but not in the eighth grade experiment) such that students in the SimCalc replacement units rated as low had lower gain scores than did students rated as medium or high.
Geographic region. We found no differences across geographic region in pretest scores or in gain scores in the main experiments. In the Seventh grade quasi-experiment, however, there was an interaction such that students in Region 1 using SimCalc in Year 2 had lower learning gains than their counterparts in other regions.
Campus poverty. Whereas campus poverty, measured at the school level as percentage of students qualifying for free or reduced-price lunch, was a strong negative predictor of pretest scores, it did not predict gains in the main experiments. In the seventh grade quasi-experiment, however, there was an interaction such that in Year 2, when students used SimCalc, this was a negative predictor of learning gains.

Notable implementation findings:

Across the studies, most implementation factors showed inconsistent relationships to student gains. However, some notable implementation findings were as follows:

Technology use. Consistent with our intervention theory, SimCalc teachers spent more days in the computer lab than control teachers. In the eighthgrade study, the number of days spent in the computer lab was positively related to student M₂ gains.
Days spent on the unit. Across the studies, the SimCalc and control groups spent roughly the same average number of days on their units. The only statistically significant difference between groups was in the seventh-grade study, in which the SimCalc group spent slightly longer (1.8 days, not including in the analysis the outlier teacher who spent 66 days).
Topic coverage. Also consistent with our intervention theory, in both the seventh- and eighth-grade studies, in their daily logs SimCalc teachers reported covering topics more closely aligned with topics that are signature aspects of the SimCalc unit (i.e., using multiple representations and reasoning comparatively about more than one function).

Using our teacher MKT assessments that had been rigorously designed and developed to assess the content knowledge that teachers would need to teach each unit, we examined how teacher MKT may be impacted by teachers’ participation in the study and/or impact the enactment of the unit. Key findings were as follows:

Teachers were normally and widely distributed in their MKT scores.
None of the teacher demographic or school-level variables that we measured correlated with MKT, suggesting that MKT is not a proxy for another construct.
From the beginning to the end of each study, teachers’ overall MKT grew modestly.
MKT moderately predicted student gain on the M₂ subscale in the treatment group in the seventh-grade year 1 study (β = 0.13, p < .01, using HLM), but this finding was not replicated in the seventh-grade quasi-experiment (β = 0.09, ns) or eighth-grade study (β = 0.04, ns).
MKT did not predict any of the unit implementation variables that we had found were most impactful for M2 student learning (computer use intensity, cognitive complexity of learning goals, topic focus).

An analysis of student workbooks revealed that they vary in completeness and accuracy. Prior knowledge predicts both completeness and accuracy (students with lower prior knowledge complete less of the workbook and do so with less accuracy) and completeness and accuracy predict student learning gains on our post-test. This suggests that doing the workbook (which entails using the software) was important to student outcomes, validating the SimCalc program theory. Further, it suggests that greater equity might be achieved by supporting students with lower prior knowledge to complete more of the workbook and to give feedback when they do so less accurately.
We examined the low-low effect: students who are rated low-achieving by their teachers do particularly poorly if they are in a classroom of low prior knowledge peers. For each study, we ran an HLM model of student gains, nesting students within classrooms. We then constructed the model using classroom mean 3 pretest as a predictor at the classroom level and indicator variables of teacherrated student achievement level (low and middle levels, with high level as the reference category) as predictors at the student level. To test for the low-low effect, we examined the coefficient for the interaction between classroom pretest and the indicator for low-achieving student. This coefficient was positive and significant in both the seventh-grade study (β = 0.29, p < .05) and the eighthgrade study (β = 0.40, p < .001), indicating the presence of the low-low effect. We have been exploring factors that may produce the low-low effect across various studies and have tentatively concluded that the overall mediating variable is the degree to which the classroom focuses on student thinking. A focus on student thinking depends both on what students bring to the classroom and how teachers conduct the classroom, with complex processes involving prior knowledge, affect, classroom pace, classroom discourse, etc.
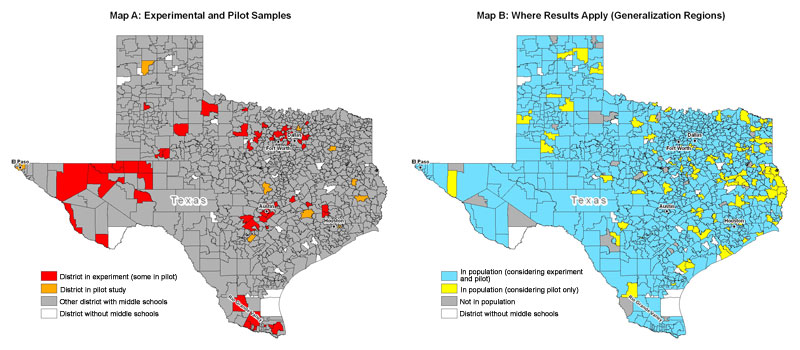
With Larry Hedges and Elizabeth Tipton, we conducted a generalizability analysis and found that our SimCalc results readily generalize to most of Texas. This analysis was based on a novel propensity score matching method that Tipton and Hedges have been developing. The images below show the geographic regions in which we collected data and show that while we collected data in just a few regions, our results generalize to most of the state.

Additional findings from co-PIs

Students gained on the same sorts of items in both the control and the treatment group but gained more in the treatment group (Hegedus).
Some test items appeared to detect common misconceptions (rather than random choice of wrong answers), and the SimCalc treatment was more effective in addressing these misconceptions (Hegedus).
Despite the use of the same materials and activities, there was a great deal of variety in the classroom talk of the four case-study teachers in the content and its degree and depth of connectedness (Empson).
The majority of content in classroom talk was connected simply (e.g., “steeper means faster”) and did not include reasons or elaborations (Empson).
Whole-group discussion and question-and-answer recitation tended to be dominated by a small group of middle- and high-achieving students (Empson).
Two markers of teacher discourse with students—responsiveness to students and cognitive demand—predicted student gains in a sample of 13 treatment teachers (Pierson).
We explored the phenomenon of racial matching between students and their teacher but found that effects resolve into a simple advantage for white students. This calls into question existing racial matching theories (Stroter).
The uses of laughter vary in the classroom, may be a good marker for classroom norms and expectations, and may predict student learning gains (Tatar).
The effective availability of material resources to the student may be constrained by a number of factors including but not limited to physical circumstances, school policy, teacher policy, and/or teacher practice (Tatar).
In a survey study of diffusion in the year following the research, of the 42% of individuals who responded to the diffusion survey, 48% of respondents were still using SimCalc (stick) and 67% had shared information with a colleague about the materials (spread). Overall, given that no incentives were given to teachers for these behaviors and the materials were not formally adopted or required in their schools, we find this rate of continued use to be encouraging. An analysis of which aspects of materials teachers were using revealed that they were using a coherent core sequence of lessons that were close to the designers’ intent (Hegedus).
Also in the diffusion research, “Perceived coherence” of the SimCalc materials to teachers’ instructional goals and accountability requirements was the major factor in stick and spread, with “help seeking” further contributing to spread. To our surprise, neither technology availability nor institutional barriers appeared to be correlated with stick or spread. This could be because the teachers in the study had sufficient technology and had already addressed institutional barriers through their prior participation (Hegedus).
Also in the diffusion research, three factors were important for sustainability: (1) teachers perceive the professional development they received as aligning with the value of the SimCalc materials in the classroom, (2) teachers see the integration of software and curriculum valuable, and (3) teachers see the professional development they received as valuable to their teaching. SimCalc materials were more likely to stick and spread with teachers who reported agreement with these factors (Hegedus).